В содержательном подходе количество информации, заключенное в сообщении, определяется объемом знаний, который это сообщение несет получающему его человеку.

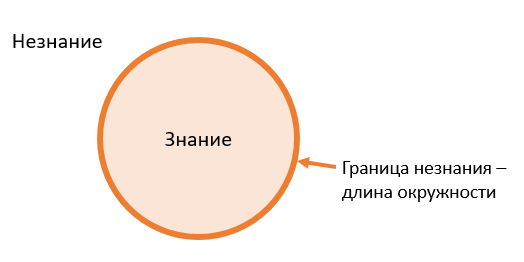
Процесс познания можно изобразить в виде расширяющегося “круга знания“, всё что за пределами круга – область незнания.

И вот здесь как раз проявляется парадокс:

Чем больше знаешь, тем больше понимаешь, что ничего не знаешь…

Другими словами, по мере получения знаний, человек раздвигает границы познания, но при этом всё больше осознает объёмы своего незнания.

Например, знания выпускника школы гораздо больше чем знания первоклассника, но и граница его незнания также существенно больше, т.е. старшеклассник при подготовке к выпускным экзаменам обнаруживает непонимание некоторых законов или правил и вынужден их восполнять. Тогда как первоклассник вообще ничего не знает об этих законах и правилах.

Подход к измерению информации, как способу уменьшения неопределённости знания, позволяет измерять информацию, особенно это ВАЖНО для информатики, которая изучает процессы хранения и передачи информации.

Информацию можно рассматривать как набор сообщений.

Сообщение – это форма представления каких-либо сведений в виде речи, текста, изображений, графиков, таблиц и т.д.

Информация – это знания, которые мы получаем из внешнего мира. Количество информации, заключенное в сообщении, должно быть тем больше, чем больше оно пополняет наши знания.

1 бит – минимальная единица измерения количества информации.

Сообщение, уменьшающее неопределенность знания в два раза, несет 1 бит информации.

Допустим, вы бросаете, загадывая, что выпадет: орел или решка.

Есть всего два возможных результата бросания монеты. Причем ни один из этих результатов не имеет преимущества перед другим. В таком случае говорят, что они равновероятны.

В случае с монетой перед ее подбрасыванием неопределенность знания о результате равна двум.

Игральный кубик с шестью гранями может с равной вероятностью упасть на любую из них. Значит, неопределенность знания о результате бросания кубика равна шести.

Неопределенность знания о результате некоторого события (бросание монеты или игрального кубика, жребий и др.) – это количество возможных результатов.

---

Формула Хартли:

Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных событий.

Тогда количество информации i, содержащееся в сообщении о том, что произошло одно из N равновероятных событий, можно определить из формулы Хартли:

Пример:

Шахматная доска состоит из 64 полей: 8 столбцов на 8 строк.

Какое количество бит несет сообщение о выборе одного шахматного поля?

Решение.

Поскольку выбор любой из 64 клеток равновероятен, то количество бит находится из формулы:

2^i=64,  2^i=2^6

Следовательно,  i=6 бит.