Информатика. Базовый курс

Чтобы рассмотреть участие информации в информационном процессе нужно её измерять.

Существует 2 подхода к измерению количества информации.

В содержательном подходе количество информации, заключенное в сообщении, определяется объемом знаний, который это сообщение несет получающему его человеку.

Что же такое сообщение?

Сообщение – это форма представления каких-либо сведений в виде речи, текста, изображения, графиков, таблиц и т.д.

Любое сообщение имеет вероятностную характеристику, т.е. как событие, которое может наступить с определённой долей вероятности.

Пример: Представим что в ящике лежат 2 шара (синий и красный). Перед вытаскиванием мы знаем о том что возможны 2 события:

• синий шар;
• красный шар.

Для нас эти 2 события равновероятны. После того, как шар вытащен, наступает полная определённость: какой шар – вытащен, а какой остался в ящике.

При вытаскивании одного из двух шаров мы получаем сообщение, которое приводит к уменьшению неопределённости знания в 2 раза.

Что такое Вероятность?

Если N – общее число возможных вариантов (событий), а из них интересующее нас событие может произойти k раз, то вероятность этого события можно определить по формуле:

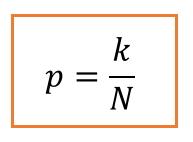
Для примера с шарами, вероятность вытаскивания одного из шаров, равна 1/2 или 0,5, другими словами они равновероятны. Если, к примеру, в ящике лежали бы все шары одного цвета, синего, то вероятность была бы равна 1.

Т.е. событие достоверно, если мы достали синий шар, и событие невозможно, если из 2-х синих шаров мы достали красный.

Теперь усложним задачу: Представим, что у нас в ящике лежат: 3 красных шара и 1 синий. Вытаскиваем 1 шар, т.е. у нас возникает одно из возможных событий, учитывая, что красных шаров больше, мы понимаем что скорей всего будет вытащен именно красный шар, но может быть и синий. Тогда по формуле посчитает вероятность соответствующих событий:

p(кр.)=1/4=0,25;      p(син.)=3/4=0,75

Какая информация для нас будет ценнее? О том что мы вытащили красный шар или синий?

Конечно красный, потому что мы этим сообщением получили полное знание о том, что в коробке остались только синие шары. Тогда как сообщение о том, что мы вытащили синий шар также уменьшает неопределённость знания, но не даёт нам полного знания.

Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить так:

Чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.

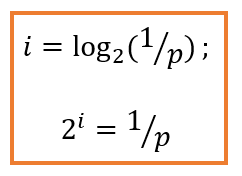
Если событие достоверно, его вероятность равна 1, то оно неинформативно, т.е. количество информации в нём равно 0. Чем меньше вероятность какого-либо события, тем большую ценность имеет информация об этом событии и тем больше будет значение i.

Единицей измерения количества информации является бит (от англ. bit – binary digit – двоичная цифра).

1 бит — количество информации, которое необходимо для того чтобы различить два равновероятных события.

Для примера с двумя шарами, докажем что сообщение об одном из двух равновероятных событий несёт 1 бит информации:

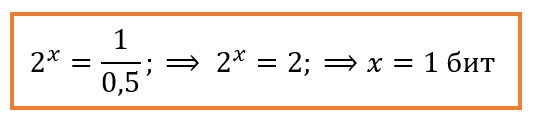
Количество информации можно рассчитать методом Р. Хартли и К.Шеннона:

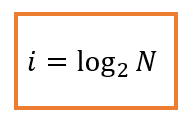
Американский инженер Р. Хартли в 1928 году рассматривал процесс получения информации как выбор одного сообщения из заданного множества N равновероятных сообщений, а количество информации в одном сообщении i определял как двоичный логарифм N.

Например, при угадывании числа из набора (1……100), мы получим:

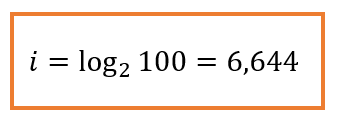
Получается, что сообщение о верно угаданном числе содержит 6,644 бит информации.

Этот метод расчёта верен, если мы имеет равновероятные события.

Для решения задач с неодинаковой вероятностью возможных событий используется формула Шеннона:

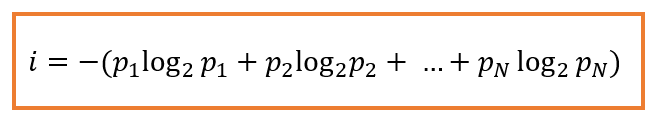
Для ситуации с 4 шарами, получим (для расчётов логарифмов можно воспользоваться он-лайн калькулятором):

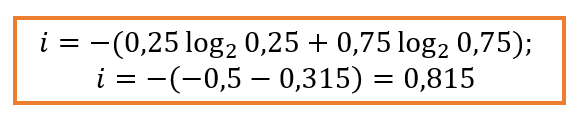
Ответ: 0,815 бит.

Таким образом, мы определили количество информации (бит), содержащейся в сообщении: “Мы достали ….. шар из корзины“.

Для того чтобы получить информацию о том, что мы достали синий шар, подставим данные в нашу формулу и получим:

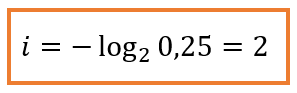
Ответ: 2 бита.

Этого и следовало ожидать, ведь жёлтых шаров в 3 раза больше, а информации о том, что “Мы достали синий шар из корзины“, мы получили больше, так как эта ситуация менее вероятна, а значит, более неожиданна.

Следовательно, информация о том, что случилось это событие уменьшает наше незнание в два раза.

1 бит — минимальная единица измерения количества информации.

Сообщение, уменьшающее неопределенность знания в два раза, несет 1 бит информации.

Допустим, вы бросаете монету, загадывая, что выпадет: орел или решка.

Есть всего два возможных результата бросания монеты. Причем ни один из этих результатов не имеет преимущества перед другим. В таком случае говорят, что они равновероятны.

В случае с монетой перед ее подбрасыванием неопределенность знания о результате равна двум.

Игральный кубик с шестью гранями может с равной вероятностью упасть на любую из них. Значит, неопределенность знания о результате бросания кубика равна шести.

Неопределенность знания о результате некоторого события (бросание монеты или игрального кубика, жребий и др.) — это количество возможных результатов.

---

Задание 1:

При игре в кости используются 2 кубика с шестью гранями. Сколько бит информации получает игрок при бросании кубиков?

---

Формула Хартли:

Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных событий.

Тогда количество информации i, содержащееся в сообщении о том, что произошло одно из N равновероятных событий, можно определить из формулы Хартли:

Пример:

Шахматная доска состоит из 64 полей: 8 столбцов на 8 строк.

Какое количество бит несет сообщение о выборе одного шахматного поля?

Решение.

Поскольку выбор любой из 64 клеток равновероятен, то количество бит находится из формулы:

2^i=64,  2^i=2^6

Следовательно,  i=6 бит.

---

Задание 2:

1. В мешке лежат 64 монеты. Сообщение о том, что достали золотую монету, несёт 4 бита информации. Сколько золотых монет в мешке?

2. В ящике лежат 8 синих и 24 белых шаров. Сколько информации несёт сообщение о том, что достали чёрный шар?

3. В мешке Деда Мороза четыре вида конфет, все они одинаковые по форме и весу, но с разной начинкой. 16 конфет – 1-го вида, 8 конфет – 2-го вида, 8 – 3-го вида и 32 конфеты – 4-го.  Сколько бит содержится в информации: “Дед мороз достал конфету i-го вида.”