Информатика. Базовый курс

Система счисления — это правила записи чисел с помощью специальных знаков — цифр, а также соответствующие правила выполнения операций с этими числами.

Человечество не сразу пришло к использованию концепции использования разрядов числа, которую мы используем сегодня для ведения счёта.

Унарная (лат. unus – один) – одна цифра обозначает единицу (1 день, 1 камень, 1 баран, …).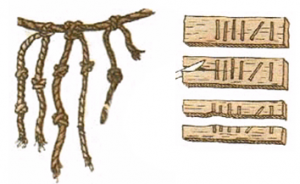

Примеры единичной системы счисления: счёт на пальцах, кости с зарубками, узелковое письмо.

Недостатки: можно использовать только натуральные числа, а для записи больших чисел, как, например,  1 млн. – требуется много знаков.

Позиционная система счисления – значение цифры зависит от её места в записи числа. Например, числа 123 и 321 – состоят из одних и тех же цифр, но, поскольку, стоят эти цифры в разных разрядах, мы читаем их значения по-разному.

Непозиционные системы счисления строятся по другому принципу. Например, известная римская система счисления имеет набор основных символов (цифр): I – 1; V – 5; X – 10; L – 50; C – 100 и т.д. и каждое число представляется как комбинация этих символов. Например, число 78 запишется так:

LXXVIII

В римской системе счисления смысл каждого символа не зависит от того места, на котором он стоит. Так, в записи числа 78, цифра X, участвуя 2 раза, каждый раз означает одну и ту же величину – 10 единиц.

---

Древнеегипетская десятичная система счисления

Человечество во все времена стремилось понять как устроен материальный мир. Но освоить качества окружающих нас объектов и их свойства невозможно без систем мер и измерений. Древнеегипетская цивилизация подарила человечеству такие математические открытия, как золотое сечение, площадь круга. Они были первыми, кто додумался до дискретности или частей целого (долей).

Одной из первых десятичных систем счисления можно считать древнеегипетскую систему счисления. Для обозначения цифр: 1; 10; 100; 1000 и т.д. египтяне использовали специальные символы. Так I – (черта) означала единицу; ∩ – (хомут) – 10; верёвочное кольцо означало – 100, а цветок лотоса – 1000. Указательный палец – 100 000, лягушка – 100 000, человек – 1 млн.  Смысл каждого символа не зависел от места, на котором он стоит. Записать большое число, например, 1 миллион, можно было с помощью одного символа, но для записи 1 000 000 – 1, т.е. 999 999, потребовалось бы 54 символа.

Например, число 32 456 будет выглядеть: 

---

Задание 1:

Древнеегипетская задачка

В папирусе, написанном египетским писцом Ахмесом, есть задачка: разделить семь хлебов между восемью людьми за минимальное число разрезов. (разрез – разделение хлеба или его части – пополам). Как решить задачу и сколько разрезов понадобится?

---

Вавилонская система счисления

Одной из древнейших систем счисления считается вавилонская нумерация. Ещё 40 веков назад в Древнем Вавилоне была создана особая система записи чисел. Песцы, именно так называли специально обученных грамоте людей, использовали глиняные таблички, записи на них наносились остро заточенной палочкой.

Таблички сохранились разного содержания, но особую важность представляют таблицы с вычислениями.

В отличие от привычной нам десятичной записи числа, где мы используем всего 10 цифр, вавилоняне использовали аж 60. Поэтому вавилонскую систему счисления принято считать шестидесятеричной.

С другой стороны, вавилоняне использовали концепцию разрядов, поэтому могли записывать даже астрономические числа. Вавилонскую систему счисления можно смело отнести к позиционным системам счисления. Т.е. в ней, как и в нынешней десятичной системе, одна и та же цифра могла обозначать разные числа, в зависимости от места, занимаемого этой цифрой. Но, в вавилонской системе счисления, ту же роль, которую у нас играет число 10, играло число 60.

Для записи числа использовались 2 основных знака:

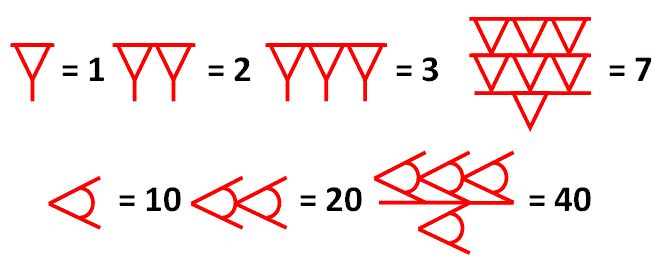
Для того, чтобы стать полноценной позиционной системой счисления, вавилонской не
хватало “нуля”, поначалу люди, при записи оставляли просто пустое место, но, в последствие, знак появился:

Теперь несложно будет понять что означает надпись:

 12 × 60³ + 0 × 60² + 21 × 60¹ + 32 × 60° = 2 592 000 + 0 + 1260 + 32 = 2 593 292

---

Задание 2:

Какое число записано в вавилонской системе счисления?

---

Древнерусская буквенная цифирь

В Древней Руси числа записывались с помощью букв алфавита, поэтому её называли буквенной цифирью. Но, для того, чтобы отличать буквы от цифр, использовался специальный знак: “~” – титло. Если над буквой стоит знак “~”, тогда читают цифру. Фрагмент чисел древних славян можно увидеть на циферблате Суздальского кремля.

Всего в древнерусской числовой системе использовалось 27 цифр:

Единицы: от 1 до 9; Десятки: от 10 до 90; Сотни: от 100 до 900.

Таким образом, запись чисел выглядела довольно компактной. Известно, что чем меньше цифр используется в системе счисления, тем длиннее будет запись чисел в ней.

 

Чтобы записать 3-х значное число, достаточно выписать соответствующие буквы-цифры слева направо. Например, число 546 будет записано так: .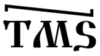

У каждой цифры свой вес и место в записи числа она будет занимать строго своё. Тогда возникает ограничение: максимальное число, которое можно записать – 999.

Как же быть с числами > 1000? Славяне использовали специальный знак “҂”, означающий тысячу, а цифра, стоящая после этого знака определяет количество тысяч.

Так, число: 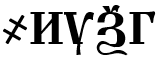 соответствует 8 463

 

---

Задание 3: